กรอบการประเมินด้านคณิตศาสตร์

PISA 2022 ให้นิยาม “ความฉลาดรู้ด้านคณิตศาสตร์” ไว้ดังนี้

ความฉลาดรู้ด้านคณิตศาสตร์ (Mathematical literacy) หมายถึง สมรรถนะในการให้เหตุผลทางคณิตศาสตร์ร่วมกับการคิด ใช้ และตีความคณิตศาสตร์ เพื่อแก้ปัญหาในบริบทของชีวิตจริงที่หลากหลาย รวมถึงการใช้มโนทัศน์ วิธีการ ข้อเท็จจริง และเครื่องมือทางคณิตศาสตร์ในการอธิบาย และคาดการณ์สถานการณ์ต่าง ๆ โดยสมรรถนะข้างต้นจะช่วยให้บุคคลเข้าใจถึงบทบาทของคณิตศาสตร์ และตัดสินใจบนพื้นฐานของข้อมูลและเหตุผลที่เหมาะสม ซึ่งเป็นสิ่งจำเป็นสำหรับพลเมืองในศตวรรษที่ 21 ที่ต้องคิดอย่างไตร่ตรอง สร้างสรรค์ และมีส่วนร่วมต่อสังคมส่วนรวม

จากนิยามความฉลาดรู้ด้านคณิตศาสตร์ PISA ได้กำหนดกรอบการประเมินด้านคณิตศาสตร์ ซึ่งครอบคลุม 3 องค์ประกอบ ได้แก่

1. การให้เหตุผลทางคณิตศาสตร์ (Mathematical reasoning) และการแก้ปัญหา (Problem solving) ที่บุคคลใช้เชื่อมโยงคณิตศาสตร์กับชีวิตจริง เพื่อนำไปสู่การแก้ปัญหาโดยใช้ความรู้และกระบวนการทางคณิตศาสตร์
2. เนื้อหาทางคณิตศาสตร์ (Mathematical content) ที่บุคคลนำมาใช้ในการแก้ปัญหา
3. บริบท (Context) เป็นสถานการณ์ที่เกี่ยวข้องกับชีวิตจริงและทักษะที่สำคัญสำหรับศตวรรษที่ 21 ซึ่งสัมพันธ์กับความฉลาดรู้ด้านคณิตศาสตร์

โดยแต่ละองค์ประกอบมีความสัมพันธ์กัน ดังแสดงในรูป 1

รูป 1 แสดงความสัมพันธ์ระหว่างการให้เหตุผลทางคณิตศาสตร์ วัฏจักรการแก้ปัญหา เนื้อหาทางคณิตศาสตร์ บริบท และทักษะแห่งศตวรรษที่ 21 ตามกรอบการประเมินคณิตศาสตร์ PISA 2022

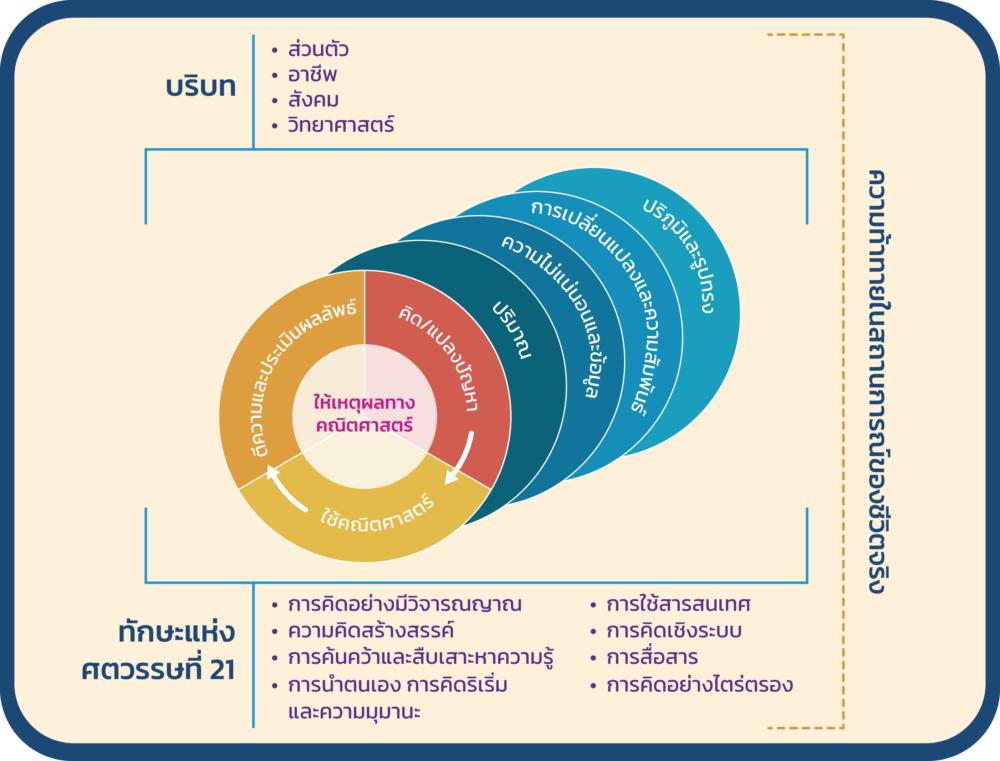
รูป 1 แสดงให้เห็นว่า นักเรียนต้องสามารถนำความรู้จากเนื้อหาทางคณิตศาสตร์ มาใช้แก้ปัญหาในบริบทที่ท้าทายหรือแก้ปัญหาที่พบเจอในชีวิตจริง เริ่มตั้งแต่การแปลงสถานการณ์ปัญหาให้อยู่ในรูปแบบที่สามารถใช้คณิตศาสตร์ในการแก้ปัญหาได้  ใช้หลักการ วิธีการ และเลือกใช้เครื่องมือทางคณิตศาสตร์เพื่อแก้ปัญหานั้น จากนั้นตีความและประเมินผลลัพธ์ให้อยู่ในบริบทของชีวิตจริง ซึ่งในแต่ละกระบวนการแก้ปัญหาต้องอาศัยการให้เหตุผลทางคณิตศาสตร์ทั้งสิ้น รวมถึงคิดอย่างไตร่ตรองถึงกระบวนการแก้ปัญหาและผลลัพธ์ที่ได้จากการประเมินและตัดสินความน่าเชื่อถือของข้อมูล นอกจากนี้ นักเรียนยังต้องอาศัยแนวคิดเชิงคำนวณ (Computational thinking) มาประยุกต์ใช้ในการแก้ปัญหา ซึ่งประกอบด้วย การพิจารณารูปแบบ การแบ่งปัญหาใหญ่เป็นปัญหาย่อย การเลือกใช้เครื่องมือคำนวณที่สามารถช่วยในการวิเคราะห์หรือแก้ปัญหา และการออกแบบขั้นตอนวิธีในการแก้ปัญหา

องค์ประกอบที่ 1 การให้เหตุผลทางคณิตศาสตร์และการแก้ปัญหา

การให้เหตุผลทางคณิตศาสตร์

การให้เหตุผลทางคณิตศาสตร์ เกี่ยวข้องกับการประเมินสถานการณ์ การเลือกกลยุทธ์ที่ใช้ในการแก้ปัญหา การสรุปที่สมเหตุสมผล การปรับปรุงและอธิบายที่มาของคำตอบ และการตระหนักรู้ถึงวิธีการประยุกต์ใช้วิธีแก้ปัญหา

การให้เหตุผลทางคณิตศาสตร์ ประกอบด้วย ความสามารถหรือการแสดงพฤติกรรมต่อไปนี้

• ระบุ ตระหนักรู้ จัดระบบ เชื่อมโยง และแสดงแทนสิ่งที่เกี่ยวข้อง
• สร้าง คิดเชิงนามธรรม ประเมิน สรุปความ แสดงเหตุผล อธิบาย และแก้ต่าง
• ตีความ ตัดสินใจ วิจารณ์ โต้แย้ง และทำให้เหมาะสม

ความสามารถในการให้เหตุผลอย่างสมเหตุสมผล และการอ้างเหตุผลที่ไม่ลำเอียงและมีความน่าเชื่อถือ เป็นทักษะที่มีความสำคัญมากขึ้นในโลกยุคปัจจุบัน  คณิตศาสตร์เป็นศาสตร์ที่เกี่ยวข้องกับสัญลักษณ์และแนวคิดต่าง ๆ ที่ได้มีการนิยามไว้อย่างชัดเจน ซึ่งสามารถนำมาวิเคราะห์และแปลงให้อยู่ในรูปแบบต่าง ๆ โดยใช้ “การให้เหตุผลทางคณิตศาสตร์” เพื่อให้ได้ข้อสรุปที่มีความชัดเจน  นักเรียนเรียนรู้จากคณิตศาสตร์ว่าการให้เหตุผลอย่างเหมาะสมจะทำให้ได้ผลลัพธ์และข้อสรุปที่มั่นใจได้ว่ามีความถูกต้องเป็นข้อสรุปที่สมเหตุสมผล ตั้งอยู่บนพื้นฐานของความเป็นจริง และไม่มีความลำเอียง

การให้เหตุผลทางคณิตศาสตร์มีความสำคัญอย่างมากในโลกปัจจุบัน และสามารถจำแนกได้สองลักษณะ ได้แก่  (1) การให้เหตุผลแบบนิรนัย (Deductive reasoning) เป็นการสรุปจากสมมติฐานหรือสิ่งที่ยอมรับว่าเป็นจริง การให้เหตุผลแบบนี้เป็นลักษณะเฉพาะหนึ่งของกระบวนการทางคณิตศาสตร์ และ (2) การให้เหตุผลแบบอุปนัย (Inductive reasoning) เป็นการให้เหตุผลในเชิงสถิติและความน่าจะเป็น ซึ่งในปัจจุบันมักมีความสับสนและเข้าใจผิดบ่อยครั้งระหว่างความเป็นไปได้ (Possible) และโอกาสที่น่าจะเกิดขึ้น (Probable) ทำให้หลายคนหลงเชื่อข่าวลวง  นอกจากนี้ โลกปัจจุบันยังมีความซับซ้อนมากยิ่งขึ้นและความซับซ้อนเหล่านั้นประกอบไปด้วยข้อมูลต่าง ๆ จำนวนมาก การทำความเข้าใจกับข้อมูลเหล่านั้นจึงเป็นหนึ่งในความท้าทายที่มนุษย์จะต้องพบเจอในอนาคต นักเรียนควรมีโอกาสได้ทำความคุ้นเคยกับข้อมูลในลักษณะดังกล่าว และการใช้ข้อมูลประกอบการตัดสินใจในบริบทที่มีความแปรผันและไม่แน่นอน

การให้เหตุผลทางคณิตศาสตร์ ตามกรอบการประเมินความฉลาดรู้ด้านคณิตศาสตร์ ประกอบด้วย ความเข้าใจหลักในเรื่องต่อไปนี้

• ความเข้าใจเกี่ยวกับปริมาณ ระบบจำนวน และสมบัติ
• การเห็นคุณค่าของการคิดเชิงนามธรรมและการแสดงแทนด้วยสัญลักษณ์
• การมองเห็นโครงสร้างทางคณิตศาสตร์และข้อกำหนดต่าง ๆ
• การตระหนักรู้ถึงความสัมพันธ์เชิงฟังก์ชันระหว่างปริมาณต่าง ๆ ที่แทนด้วยตัวแปร
• การสร้างและใช้ตัวแบบทางคณิตศาสตร์เพื่อทำให้เห็นสิ่งที่เกิดขึ้นในชีวิตจริง เช่น สิ่งที่เกิดขึ้นในทางวิทยาศาสตร์กายภาพ วิทยาศาสตร์ชีวภาพ สังคมศาสตร์ เศรษฐศาสตร์ และพฤติกรรมศาสตร์
• ความเข้าใจว่าการแปรผันเป็นแก่นสำคัญของวิชาสถิติ

ความเข้าใจเกี่ยวกับปริมาณ ระบบจำนวน และสมบัติ

ความเข้าใจเกี่ยวกับปริมาณ ระบบจำนวน และสมบัติ ในที่นี้หมายรวมถึงมโนทัศน์พื้นฐานของจำนวน โครงสร้างของระบบจำนวน การดำเนินการของจำนวน และสมบัติทางพีชคณิตที่มีในระบบจำนวน  นักเรียนควรเข้าใจว่าเมื่อระบบจำนวนมีขอบเขตกว้างขึ้นจะทำให้สามารถหาคำตอบของสมการที่ซับซ้อนมากขึ้นได้ ซึ่งเป็นพื้นฐานของการส่งเสริมให้นักเรียนสามารถมองเห็นความเชื่อมโยงของคณิตศาสตร์ในชีวิตจริงได้มากขึ้นไปพร้อมกับการเรียนคณิตศาสตร์ของตนเอง  อย่างไรก็ตาม จำนวนต่าง ๆ โดยตัวของมันเองยังใช้ประโยชน์ไม่ได้มากนัก สิ่งที่สามารถนำมาใช้งานได้อย่างมีประสิทธิภาพคือ ระบบจำนวน ซึ่งหมายรวมถึงการดำเนินการของจำนวนเหล่านั้น  ดังนั้น ความเข้าใจอย่างลึกซึ้งเกี่ยวกับการดำเนินการของจำนวนจึงเป็นพื้นฐานของการให้เหตุผลทางคณิตศาสตร์

ความรู้ความเข้าใจอย่างรอบด้านเกี่ยวกับปริมาณและระบบจำนวนจะช่วยส่งเสริมการให้เหตุผลในการประยุกต์ใช้คณิตศาสตร์ในชีวิตจริงได้

การเห็นคุณค่าของการคิดเชิงนามธรรมและการแสดงแทนด้วยสัญลักษณ์

แนวคิดพื้นฐานของคณิตศาสตร์เกิดจากประสบการณ์ต่าง ๆ ของมนุษย์และความจำเป็นที่ต้องสร้างความสัมพันธ์ กำหนดลำดับเหตุการณ์ และคาดการณ์จากประสบการณ์เหล่านั้น  หลายสิ่งในทางคณิตศาสตร์เป็นแบบจำลองของสิ่งที่อยู่ในชีวิตจริง หรืออย่างน้อยก็สะท้อนมุมมองบางด้านของชีวิตจริง การคิดเชิงนามธรรมประกอบด้วยการพิจารณาโครงสร้างของสิ่งต่าง ๆ แล้วนำมาสร้างเป็นความสัมพันธ์ระหว่างสิ่งเหล่านั้นบนพื้นฐานของโครงสร้างที่คล้ายคลึงกัน สำหรับคณิตศาสตร์ในระดับโรงเรียน การคิดเชิงนามธรรมคือ การเชื่อมโยงความสัมพันธ์ระหว่างสิ่งที่เป็นรูปธรรมไปสู่การแทนด้วยสัญลักษณ์และการดำเนินการ รวมถึงอัลกอริทึมและการสร้างแบบจำลองทางความคิด  ความสามารถในการคิดเชิงนามธรรมนี้มีบทบาทต่อการทำความเข้าใจความหมายในบริบทที่เป็นนามธรรมของเทคโนโลยี ซึ่งเป็นทักษะการคิดเชิงคำนวณที่สำคัญทักษะหนึ่ง

นักเรียนสามารถใช้การแสดงแทนได้หลากหลายรูปแบบ ทั้งในรูปแบบข้อความ สัญลักษณ์ กราฟ ตัวเลข เรขาคณิต และการเขียนโปรแกรม เพื่อจัดระบบและสื่อสารความคิดเชิงคณิตศาสตร์ของตนเองการแสดงแทนในรูปแบบต่าง ๆ นี้ ช่วยให้เราสามารถนำเสนอแนวคิดทางคณิตศาสตร์ในรูปแบบที่สั้น กระชับ ซึ่งนำไปสู่อัลกอริทึมที่มีประสิทธิภาพ การแสดงแทนยังเป็นองค์ประกอบหลักที่สำคัญของการสร้างตัวแบบทางคณิตศาสตร์ ช่วยให้นักเรียนสามารถแปลงปัญหาในชีวิตจริงให้อยู่ในรูปตัวแบบทางคณิตศาสตร์

การเห็นคุณค่าของการคิดเชิงนามธรรมและการแสดงแทนด้วยสัญลักษณ์จะช่วยส่งเสริมการให้เหตุผลในการประยุกต์ใช้คณิตศาสตร์ในชีวิตจริง โดยจะช่วยให้นักเรียนสามารถขยายแนวคิดที่เฉพาะเจาะจงของสถานการณ์หนึ่งไปสู่แนวคิดที่มีลักษณะทั่วไป และสามารถอธิบายสิ่งเหล่านี้ได้อย่างมีประสิทธิภาพ

การมองเห็นโครงสร้างทางคณิตศาสตร์และข้อกำหนดต่าง ๆ

โครงสร้างทางคณิตศาสตร์มีความสัมพันธ์อย่างมากกับการแสดงแทนด้วยสัญลักษณ์ ซึ่งควรใช้เท่าที่จำเป็นเพื่อสื่อความหมายของสัญลักษณ์นั้น การมองเห็นโครงสร้างเป็นวิธีหนึ่งของการค้นหาและจดจำความหมายของการแสดงแทนที่เป็นนามธรรม ความสามารถในการมองเห็นโครงสร้างทางคณิตศาสตร์เป็นเครื่องช่วยเชิงมโนทัศน์ที่สำคัญอันจะนำไปสู่ความรู้เชิงกระบวนการ

ความสามารถในการมองเห็นโครงสร้างทางคณิตศาสตร์จะช่วยส่งเสริมการให้เหตุผลในการประยุกต์ใช้คณิตศาสตร์ในชีวิตจริง โดยจะช่วยให้นักเรียนสามารถประยุกต์ความรู้เกี่ยวกับสถานการณ์หรือปัญหาในบริบทหนึ่งไปใช้กับสถานการณ์หรือปัญหาในอีกบริบทหนึ่งที่มีโครงสร้างคล้ายคลึงกัน

การตระหนักรู้ถึงความสัมพันธ์เชิงฟังก์ชันระหว่างปริมาณต่าง ๆ ที่แทนด้วยตัวแปร

ความสัมพันธ์ระหว่างปริมาณต่าง ๆ ที่แทนด้วยตัวแปร แสดงได้ด้วยสมการ กราฟ ตาราง หรือข้อความ และขั้นตอนที่สำคัญในการเรียนรู้คือ การแทนความสัมพันธ์ด้วยฟังก์ชันพร้อมโดเมนและโคโดเมน ตลอดจนการหาผลลัพธ์จากสิ่งที่นำเข้า นอกจากนี้ กราฟของฟังก์ชันยังเป็นเครื่องมือที่สำคัญในการสำรวจแนวคิดเกี่ยวกับอัตราการเปลี่ยนแปลง กราฟจึงเป็นเครื่องมือสำหรับทำความเข้าใจฟังก์ชันซึ่งเป็นความสัมพันธ์ระหว่างปริมาณต่าง ๆ ที่แทนด้วยตัวแปร

การตระหนักรู้ถึงความสัมพันธ์เชิงฟังก์ชันระหว่างตัวแปรต่าง ๆ ในการประยุกต์ใช้คณิตศาสตร์ในชีวิตจริงจะช่วยส่งเสริมการให้เหตุผลของนักเรียน โดยทำให้นักเรียนมุ่งความสนใจไปที่ความเชื่อมโยงและการมีปฏิสัมพันธ์ระหว่างตัวแปรต่าง ๆ ที่ส่งผลต่อสถานการณ์นั้น ๆ

การสร้างและใช้ตัวแบบทางคณิตศาสตร์เพื่อทำให้เห็นสิ่งที่เกิดขึ้นในชีวิตจริง

ตัวแบบเป็นการนำเสนอกรอบแนวคิดในอุดมคติของสถานการณ์ในชีวิตจริง  ตัวแบบอาจนำเสนอกรอบแนวคิดที่เป็นการประมาณค่าหรือการตั้งสมมติฐานเกี่ยวกับสถานการณ์ที่ศึกษา หรืออาจนำเสนอรูปอย่างง่ายของสิ่งที่สนใจ ตัวแบบทางคณิตศาสตร์ถูกสร้างให้อยู่ในรูปภาษาทางคณิตศาสตร์และมีการใช้เครื่องมือและความรู้ต่าง ๆ ทางคณิตศาสตร์ที่หลากหลาย เช่น เลขคณิต พีชคณิต หรือเรขาคณิต โดยใช้สิ่งเหล่านี้ในการกำหนดแนวคิดหรือทฤษฎีของปรากฏการณ์ที่ศึกษาเพื่อวิเคราะห์และประเมินข้อมูล โดยตรวจสอบว่าตัวแบบนั้นใช้กับข้อมูลที่มีอยู่ได้หรือไม่ และเพื่อสร้างข้อคาดการณ์  นอกจากนี้ เราใช้ตัวแบบเพื่อสร้างสถานการณ์จำลอง โดยสร้างให้ตัวแบบแสดงผลการวิเคราะห์ข้อมูลที่มีการเปลี่ยนแปลงไปในช่วงระยะเวลาหนึ่ง หรือด้วยการป้อนข้อมูลที่มีความหลากหลายเข้าไป  เมื่อเราสามารถสร้างสถานการณ์จำลองได้ เราจะสามารถสร้างข้อคาดการณ์ ศึกษาผลกระทบที่เกิดขึ้น และประเมินความเหมาะสมและความแม่นยำของตัวแบบนั้นได้ ขั้นตอนและกระบวนการสร้างตัวแบบนั้นต้องคำนึงถึงความจำเป็นของตัวแปรเสริมที่มีอยู่ในชีวิตจริงซึ่งมีผลกระทบต่อตัวแบบ

การสร้างตัวแบบทั่วไปและตัวแบบทางคณิตศาสตร์จะช่วยส่งเสริมการให้เหตุผลของนักเรียนในการประยุกต์ใช้คณิตศาสตร์ในชีวิตจริง โดยจะช่วยกระตุ้นให้นักเรียนมุ่งความสนใจไปยังสิ่งที่สำคัญที่สุดของสถานการณ์และช่วยจำกัดขอบเขตของปัญหาให้ชัดเจน

ความเข้าใจว่าการแปรผันเป็นแก่นสำคัญของวิชาสถิติ

วิชาสถิติตั้งอยู่บนแนวคิดพื้นฐานเรื่องการจัดการกับความแปรผัน  ในปัจจุบันผู้คนต้องจัดการกับสถานการณ์เหล่านี้อยู่เสมอ แต่พวกเขามักจะเพิกเฉยต่อความแปรผัน และผลลัพธ์ที่ตามมาคือ การมองสถานการณ์ในภาพรวมกว้าง ๆ ซึ่งบ่อยครั้งทำให้เกิดความผิดพลาดหรือนำไปสู่ความเข้าใจที่ผิด และอาจก่อให้เกิดความเสียหายอย่างรุนแรงได้  ความเอนเอียงที่เกิดขึ้นในทางสังคมศาสตร์มักจะเกิดจากการละเลยถึงแหล่งที่มาและความสำคัญของความแปรผันในสิ่งที่ศึกษา

สถิติในหลายกรณีเป็นการค้นหารูปแบบในบริบทที่มีความแปรผันสูง หรือเป็นการค้นหา “ความจริง” ซึ่งไม่ใช่ค่าจริงตามความหมายของคณิตศาสตร์ แต่เป็นการหาค่าประมาณในบริบทของความน่าจะเป็นควบคู่ไปกับการประมาณค่าความคลาดเคลื่อนที่พบในกระบวนการ  ในที่สุดแล้ว ผู้ที่ต้องตัดสินใจจะไม่สามารถรู้ได้อย่างแน่นอนว่าค่าจริงดังกล่าวคืออะไร แต่ค่าประมาณที่หามาได้นั้นจะอยู่ในช่วงของค่าที่เป็นไปได้ถ้ากระบวนการดีขึ้นจะทำให้ได้ผลลัพธ์ดีขึ้นด้วย เช่น การใช้ข้อมูลจำนวนมากขึ้น จะช่วยให้ช่วงของค่าที่เป็นไปได้แคบลง แต่ก็ยังหลีกเลี่ยงการได้คำตอบเป็นช่วงไม่ได้

การเข้าใจว่าความแปรผันเป็นแก่นของวิชาสถิติจะช่วยส่งเสริมการให้เหตุผลของนักเรียนในการประยุกต์ใช้คณิตศาสตร์ในชีวิตจริง โดยจะช่วยกระตุ้นให้นักเรียนได้เผชิญกับการโต้แย้งโดยอ้างอิงข้อมูลร่วมกับการตระหนักถึงข้อจำกัดของข้อสรุปที่ได้

การแก้ปัญหา

ในการแก้ปัญหาในบริบทชีวิตจริงตามนิยามของความฉลาดรู้ด้านคณิตศาสตร์มีความเกี่ยวข้องกับกระบวนทางคณิตศาสตร์ต่อไปนี้

• การคิด/แปลงสถานการณ์ปัญหาในเชิงคณิตศาสตร์ หรือ “คิด/แปลงปัญหา” (Formulate)
• การใช้มโนทัศน์ ข้อเท็จจริง วิธีการ และการให้เหตุผลทางคณิตศาสตร์ในการแก้ปัญหา หรือ “ใช้คณิตศาสตร์” (Employ)
• การตีความ การประยุกต์ใช้ และการประเมินผลลัพธ์ทางคณิตศาสตร์ หรือ “ตีความและประเมินผลลัพธ์” (Interpret and evaluate)

การคิด/แปลงสถานการณ์ปัญหาในเชิงคณิตศาสตร์ หรือ “คิด/แปลงปัญหา” (Formulate)

คำว่า “คิด/แปลง” ตามนิยามความฉลาดรู้ด้านคณิตศาสตร์ หมายถึง สมรรถนะในการแยกแยะและ
รู้ถึงโอกาสที่จะใช้คณิตศาสตร์ และใช้ความรู้เกี่ยวกับโครงสร้างทางคณิตศาสตร์ที่จำเป็นในการแปลงสถานการณ์ให้เป็นรูปแบบทางคณิตศาสตร์  ในขั้นตอนการแปลงสถานการณ์ให้เป็นบริบททางคณิตศาสตร์ แต่ละบุคคลจะต้องพิจารณาว่าจะนำความรู้คณิตศาสตร์ส่วนใดมาวิเคราะห์ จัดการ และแก้ปัญหา  พวกเขาจะต้องแปลงสิ่งที่อยู่ในชีวิตจริงให้อยู่ในบริบทของคณิตศาสตร์ กำหนดโครงสร้าง การแสดงแทน และข้อมูลทางคณิตศาสตร์ให้กับปัญหาในชีวิตจริงนั้น โดยต้องพิจารณาและทำความเข้าใจถึงข้อจำกัดและสมมติฐานต่าง ๆ ในปัญหา กระบวนการในการคิด/แปลงสถานการณ์ปัญหาในเชิงคณิตศาสตร์นี้ ประกอบด้วยกิจกรรมต่าง ๆ เช่น

• การเลือกใช้ตัวแบบที่เหมาะสม
• การระบุมุมมองเชิงคณิตศาสตร์ของปัญหาที่อยู่ในบริบทของชีวิตจริงและการระบุตัวแปรที่สำคัญ
• การตระหนักรู้ถึงโครงสร้างทางคณิตศาสตร์ รวมถึงข้อกำหนด ความสัมพันธ์ และแบบรูป ที่อยู่ในปัญหาหรือสถานการณ์
• การจัดการสถานการณ์หรือปัญหาให้อยู่ในรูปแบบที่ง่ายและสะดวกต่อการวิเคราะห์ทางคณิตศาสตร์ เช่น ใช้วิธีการแยกส่วนประกอบ หรือแบ่งปัญหาใหญ่ให้เป็นปัญหาย่อย
• การระบุข้อจำกัดและสมมติฐาน รวมทั้งการสร้างตัวแบบทางคณิตศาสตร์
• การแสดงแทนสถานการณ์ด้วยคณิตศาสตร์ โดยใช้ตัวแปร สัญลักษณ์ แผนภาพ และตัวแบบที่เหมาะสม
• การแสดงแทนปัญหาในรูปแบบที่แตกต่าง รวมถึงการจัดโครงสร้างปัญหาตามมโนทัศน์ทางคณิตศาสตร์ และการสร้างสมมติฐานที่เหมาะสม
• ความเข้าใจและการอธิบายความสัมพันธ์ระหว่างภาษาในบริบทที่จำเพาะของปัญหากับสัญลักษณ์และภาษาที่เป็นทางการที่จำเป็นต้องใช้ในการนำเสนอปัญหานั้นในเชิงคณิตศาสตร์
• การแปลงปัญหาให้เป็นภาษาคณิตศาสตร์หรือการแสดงแทนทางคณิตศาสตร์
• การตระหนักรู้ว่าปัญหาหนึ่ง ๆ มีประเด็นที่เชื่อมโยงกับปัญหาเดิม หรือมโนทัศน์ ข้อเท็จจริง หรือวิธีการทางคณิตศาสตร์อย่างไร
• การเลือกและการใช้วิธีการและเครื่องมือคำนวณที่มีประสิทธิภาพที่สุดที่แสดงถึงความสัมพันธ์เชิงคณิตศาสตร์ที่มีอยู่ในบริบทของปัญหา
• การสร้างลำดับขั้นตอนเพื่อใช้ในการแก้ปัญหา

การใช้มโนทัศน์ ข้อเท็จจริง วิธีการ และการให้เหตุผลทางคณิตศาสตร์ในการแก้ปัญหา หรือ “ใช้คณิตศาสตร์” (Employ)

คำว่า “ใช้” ตามนิยามความฉลาดรู้ด้านคณิตศาสตร์ หมายถึง สมรรถนะในการประยุกต์ใช้มโนทัศน์ ข้อเท็จจริง วิธีการ และการให้เหตุผลทางคณิตศาสตร์ในการแก้สถานการณ์ปัญหาซึ่งได้แปลงให้อยู่ในรูปคณิตศาสตร์แล้ว เพื่อให้ได้ข้อสรุปทางคณิตศาสตร์ ในขั้นตอนการประยุกต์ใช้มโนทัศน์ ข้อเท็จจริง วิธีการ และการให้เหตุผลทางคณิตศาสตร์ในการแก้ปัญหานั้น แต่ละบุคคลต้องแสดงการดำเนินการตามกระบวนการทางคณิตศาสตร์ที่จำเป็นเพื่อให้ได้มาซึ่งผลลัพธ์และหาวิธีแก้ปัญหาทางคณิตศาสตร์ อาทิ การคำนวณเบื้องต้น การแก้สมการ การอนุมานด้วยหลักเหตุผลจากสมมติฐานทางคณิตศาสตร์ การจัดการกับสัญลักษณ์ การพิจารณาเลือกข้อมูลทางคณิตศาสตร์จากตารางหรือกราฟ การแสดงและการจัดการกับรูปเรขาคณิตสามมิติ และการวิเคราะห์ข้อมูล เป็นต้น  นักเรียนต้องดำเนินการกับตัวแบบของสถานการณ์ปัญหา สร้างข้อกำหนด ระบุความเกี่ยวข้องกับสิ่งต่าง ๆ ทางคณิตศาสตร์ และสร้างข้อโต้แย้งทางคณิตศาสตร์ กระบวนการในการใช้มโนทัศน์ ข้อเท็จจริง วิธีการ และการให้เหตุผลทางคณิตศาสตร์เพื่อแก้ปัญหานี้ ประกอบด้วยกิจกรรมต่าง ๆ เช่น

• การแสดงการคำนวณอย่างง่าย
• การสร้างข้อสรุปอย่างง่าย
• การเลือกใช้กลยุทธ์ที่เหมาะสม
• การออกแบบกลยุทธ์ต่าง ๆ และนำกลยุทธ์เหล่านั้นไปใช้เพื่อหาวิธีแก้ปัญหาทางคณิตศาสตร์
• การใช้เครื่องมือทางคณิตศาสตร์และเทคโนโลยีเพื่อช่วยหาคำตอบที่เป็นค่าแน่นอนหรือค่าประมาณ
• การใช้ข้อเท็จจริง กฎ อัลกอริทึม และโครงสร้างทางคณิตศาสตร์ในการหาคำตอบ
• การจัดการกับตัวเลข ข้อมูลและสารสนเทศที่นำเสนอด้วยกราฟและในเชิงสถิติ นิพจน์และสมการเชิงพีชคณิต และการแสดงแทนทางเรขาคณิต
• การสร้างแผนภาพ กราฟ และแบบจำลองสถานการณ์ทางคณิตศาสตร์ และการสร้างและสกัดข้อมูลทางคณิตศาสตร์จากสิ่งเหล่านี้
• การใช้การแสดงแทนในรูปแบบต่าง ๆ และการปรับเปลี่ยนการแสดงแทนระหว่างรูปแบบต่าง ๆ ในกระบวนการแก้ปัญหา
• การสร้างข้อสรุปในรูปทั่วไปและข้อคาดการณ์ที่มีพื้นฐานมาจากผลลัพธ์ที่ได้จากการประยุกต์ใช้กระบวนการทางคณิตศาสตร์ในการแก้ปัญหา
• การสะท้อนการอ้างเหตุผลทางคณิตศาสตร์ และการอธิบายและตรวจสอบผลลัพธ์ทางคณิตศาสตร์
• การประเมินความสำคัญของแบบรูปและลักษณะปกติของข้อมูลที่สังเกตได้ (หรือที่สร้างขึ้น)

การตีความ การประยุกต์ใช้ และการประเมินผลลัพธ์ทางคณิตศาสตร์ หรือ “ตีความและประเมินผลลัพธ์” (Interpret and evaluate)

คำว่า “ตีความและประเมิน” ตามนิยามความฉลาดรู้ทางคณิตศาสตร์ มุ่งเน้นสมรรถนะในการสะท้อนวิธีแก้ปัญหา ผลลัพธ์ หรือข้อสรุปทางคณิตศาสตร์ และตีความสิ่งเหล่านี้ในบริบทของปัญหาในชีวิตจริงที่เป็นปัญหาเริ่มต้นได้  รวมถึงการแปลความหมายของวิธีแก้ปัญหาหรือการให้เหตุผลทางคณิตศาสตร์กลับไปยังบริบทของปัญหาแล้วพิจารณาว่า ผลลัพธ์ที่ได้นั้นมีความสมเหตุสมผลและมีความหมายในบริบทของปัญหาหรือไม่  การตีความ การประยุกต์ใช้ และการประเมินผลลัพธ์ทางคณิตศาสตร์ เป็นการรวมองค์ประกอบของวัฏจักรการสร้างตัวแบบทางคณิตศาสตร์สองด้านไว้ด้วยกัน คือ “ตีความ” และ “ประเมิน”  บุคคลที่ใช้กระบวนการนี้จะต้องสร้างและสื่อสารคำอธิบายและข้อโต้แย้งในบริบทของปัญหาเริ่มต้น โดยต้องสะท้อนทั้งกระบวนการสร้างตัวแบบและผลลัพธ์ที่ได้มา  กระบวนการในการตีความ การประยุกต์ใช้ และการประเมิน
ผลลัพธ์ทางคณิตศาสตร์นี้ ประกอบด้วยกิจกรรมต่าง ๆ เช่น

• การตีความสารสนเทศที่แสดงอยู่ในรูปของกราฟและ/หรือแผนภาพ
• การประเมินผลลัพธ์ทางคณิตศาสตร์ที่สอดคล้องกับบริบทของปัญหา
• การตีความผลลัพธ์ทางคณิตศาสตร์กลับไปยังบริบทของชีวิตจริง
• การประเมินความสมเหตุสมผลของผลลัพธ์ทางคณิตศาสตร์ในบริบทของปัญหาในชีวิตจริง
• การเข้าใจว่าชีวิตจริงส่งผลกระทบต่อผลลัพธ์และวิธีคิดคำนวณในกระบวนการทางคณิตศาสตร์หรือตัวแบบทางคณิตศาสตร์อย่างไร เพื่อตัดสินใจว่าควรจะต้องปรับปรุงหรือนำผลลัพธ์ไปใช้อย่างไร
• การอธิบายเหตุผลว่าผลลัพธ์หรือข้อสรุปทางคณิตศาสตร์ที่ได้นั้นสมเหตุสมผลหรือไม่สมเหตุสมผลตามบริบทของปัญหาในชีวิตจริง
• การเข้าใจถึงขอบเขตและข้อจำกัดของแนวคิดทางคณิตศาสตร์และวิธีการแก้ปัญหาทางคณิตศาสตร์
• การวิจารณ์และการระบุข้อจำกัดของตัวแบบที่ใช้ในการแก้ปัญหา
• การใช้การคิดเชิงคณิตศาสตร์และแนวคิดเชิงคำนวณในการคาดการณ์ การแสดงหลักฐานเพื่อสนับสนุนข้อโต้แย้ง และตรวจสอบและเปรียบเทียบผลลัพธ์ที่ได้

องค์ประกอบที่ 2 เนื้อหาทางคณิตศาสตร์

ความเข้าใจในเนื้อหาทางคณิตศาสตร์ รวมถึงความสามารถที่จะนำความรู้ไปใช้ในการแก้ปัญหาได้จริงเป็นสิ่งสำคัญสำหรับพลเมืองในโลกยุคปัจจุบัน นั่นคือ การให้เหตุผลในเชิงคณิตศาสตร์ การแก้ปัญหา และการตีความสถานการณ์ในบริบทที่เกี่ยวกับเรื่องส่วนตัว อาชีพ สังคม และวิทยาศาสตร์ จำเป็นต้องใช้ความรู้และความเข้าใจในเนื้อหาคณิตศาสตร์

หมวดหมู่ของเนื้อหาทางคณิตศาสตร์ที่ใช้ในการประเมิน PISA 2022 ยังคงเป็นเช่นเดียวกับใน PISA 2012 เพื่อสะท้อนถึงปรากฏการณ์ทางคณิตศาสตร์ที่อยู่เบื้องหลังกลุ่มของปัญหาจำนวนมาก โครงสร้างทั่วไปของคณิตศาสตร์ และเนื้อหาสาระหลักในหลักสูตรของโรงเรียนโดยทั่วไป

โครงสร้างการประเมินด้านคณิตศาสตร์ครอบคลุมเนื้อหา 4 หมวดหมู่ ดังนี้

• การเปลี่ยนแปลงและความสัมพันธ์ (Change and Relationships)
• ปริภูมิและรูปทรง (Space and Shape)
• ปริมาณ (Quantity)
• ความไม่แน่นอนและข้อมูล (Uncertainty and Data)

นอกจากนี้ ใน PISA 2022 ยังได้เพิ่มหัวข้อที่เป็นจุดเน้น 4 หัวข้อ เพื่อเป็นส่วนหนึ่งของเนื้อหาทางคณิตศาสตร์ที่ใช้ประเมินในแต่ละหมวดหมู่ เนื่องจากเป็นความรู้ทางคณิตศาสตร์ที่จำเป็นในระบบเศรษฐกิจที่กำลังจะเกิดขึ้น อาทิ อุตสาหกรรมการผลิตที่ใช้เทคโนโลยีขั้นสูง โดยหัวข้อที่เป็นจุดเน้นทั้ง 4 หัวข้อ สอดคล้องกับเนื้อหาแต่ละหมวดหมู่ ดังนี้

• สถานการณ์การเพิ่มจำนวน อยู่ในหมวดหมู่การเปลี่ยนแปลงและความสัมพันธ์
• การประมาณค่าเชิงเรขาคณิต อยู่ในหมวดหมู่ปริภูมิและรูปทรง
• การจำลองสถานการณ์ด้วยคอมพิวเตอร์ อยู่ในหมวดหมู่ปริมาณ
• การตัดสินใจแบบมีเงื่อนไข อยู่ในหมวดหมู่ความไม่แน่นอนและข้อมูล

การเปลี่ยนแปลงและความสัมพันธ์

เราสามารถพบเห็นความสัมพันธ์ระหว่างวัตถุกับสภาพแวดล้อมทั้งชั่วคราวและถาวรได้หลากหลายรูปแบบจากสิ่งต่าง ๆ ที่เกิดขึ้นตามธรรมชาติและสิ่งที่มนุษย์สร้างขึ้น โดยมีการเปลี่ยนแปลงเกิดขึ้นในระบบของวัตถุที่มีความเชื่อมโยงกัน หรือในสถานการณ์ที่องค์ประกอบต่าง ๆ ส่งผลซึ่งกันและกัน ในบางกรณีการเปลี่ยนแปลงเหล่านี้เกิดขึ้นเมื่อเวลาผ่านไป และบางกรณีการเปลี่ยนแปลงของสิ่งหนึ่งหรือปริมาณหนึ่งอาจเกี่ยวข้องกับการเปลี่ยนแปลงของอีกสิ่งหนึ่งหรืออีกปริมาณหนึ่ง  บางสถานการณ์อาจเป็นการเปลี่ยนแปลงแบบต่อเนื่องหรือไม่ต่อเนื่อง  ดังนั้น เนื้อหาการเปลี่ยนแปลงและความสัมพันธ์จึงเกี่ยวข้องกับความเข้าใจการเปลี่ยนแปลงแบบต่าง ๆ และการรับรู้เมื่อมีการเปลี่ยนแปลงเกิดขึ้น เพื่อที่จะใช้ตัวแบบทางคณิตศาสตร์ที่เหมาะสมในการอธิบายและทำนายการเปลี่ยนแปลง  ในทางคณิตศาสตร์หมายถึงการสร้างตัวแบบของการเปลี่ยนแปลงและความสัมพันธ์ให้อยู่ในรูปของฟังก์ชันและสมการที่เหมาะสม รวมถึงการสร้าง การตีความ และการแสดงแทนความสัมพันธ์ด้วยสัญลักษณ์และกราฟ

การเปลี่ยนแปลงและความสัมพันธ์พบได้ในหลายเรื่อง เช่น การเพิ่มจำนวนของสิ่งมีชีวิต รูปแบบของเสียงดนตรี การเปลี่ยนแปลงของฤดูกาลและวัฏจักร แบบแผนของสภาพอากาศ ระดับการจ้างงาน และสภาวะทางเศรษฐกิจ  ในมุมมองของเนื้อหาทางคณิตศาสตร์แบบดั้งเดิม ฟังก์ชันและพีชคณิต หมายรวมถึง นิพจน์พีชคณิต สมการและอสมการ และการแสดงแทนในรูปของตารางและกราฟ ซึ่งเป็นส่วนสำคัญในการสร้างคำอธิบาย การสร้างตัวแบบ และการตีความปรากฏการณ์การเปลี่ยนแปลงต่าง ๆ  เครื่องมือเชิงคำนวณช่วยให้เราเห็นภาพและมีปฏิสัมพันธ์กับการเปลี่ยนแปลงและความสัมพันธ์ได้  ดังนั้น การรู้ว่าเครื่องมือเชิงคำนวณสามารถเป็นส่วนเสริมและเติมเต็มแนวคิดทางคณิตศาสตร์ได้เมื่อไรและอย่างไร จึงถือว่าเป็นทักษะการคิดเชิงคำนวณที่สำคัญทักษะหนึ่ง

การทำความเข้าใจภัยอันตรายของสถานการณ์ต่าง ๆ ที่เกี่ยวข้องกับการเพิ่มจำนวน เช่น การแพร่ระบาดของโรคไข้หวัดใหญ่ การแพร่กระจายอย่างรุนแรงของเชื้อแบคทีเรีย และภัยคุกคามของการเปลี่ยนแปลงภูมิอากาศ ต้องใช้ความคิดเกี่ยวกับความสัมพันธ์ทั้งความสัมพันธ์แบบเชิงเส้นและความสัมพันธ์แบบไม่เป็นเชิงเส้น ซึ่งโดยส่วนใหญ่เป็นความสัมพันธ์แบบเอกซ์โพเนนเชียล และยังมีความสัมพันธ์ในรูปแบบอื่นด้วย  ความสัมพันธ์แบบเชิงเส้นเป็นความสัมพันธ์ที่พบได้ทั่วไป ง่ายต่อการจดจำและเข้าใจ แต่การตั้งสมมติฐานว่าความสัมพันธ์ที่พบเจอนั้นเป็นความสัมพันธ์แบบเชิงเส้นในทันทีอาจทำให้เกิดความผิดพลาดร้ายแรงได้  ตัวอย่างหนึ่งของความสัมพันธ์แบบเชิงเส้นที่ทุกคนน่าจะเคยใช้คือ การประมาณระยะทางที่เดินทางได้ในระยะเวลาต่าง ๆ เมื่อกำหนดความเร็วของการเดินทางมาให้  แต่ในตัวอย่างเรื่องการแพร่ระบาดของโรคไข้หวัดใหญ่นั้น การใช้ความสัมพันธ์แบบเชิงเส้นในการอธิบายปรากฏการณ์นี้อาจจะได้ตัวเลขแสดงจำนวนผู้ป่วยที่ติดเชื้อหลังจากเริ่มการแพร่ระบาดไปแล้ว 5 วัน เป็นจำนวนที่น้อยกว่าจำนวนที่เกิดขึ้นจริงมาก ดังนั้น ความเข้าใจเรื่องความสัมพันธ์ของการเพิ่มจำนวนแบบไม่เป็นเชิงเส้น รวมถึงแบบกำลังสองและแบบเอกซ์โพเนนเชียล และความเข้าใจว่าการติดเชื้อสามารถแพร่กระจายได้อย่างรวดเร็วเพียงใดเมื่ออัตราการเปลี่ยนแปลงจำนวนผู้ป่วยที่ติดเชื้อเพิ่มสูงขึ้นในแต่ละวันจึงเป็นเรื่องที่สำคัญมาก  การแพร่ระบาดของไวรัสซิกาเป็นอีกตัวอย่างหนึ่งที่สำคัญ การรับรู้ว่าสถานการณ์นี้เป็นการเพิ่มจำนวนแบบเอกซ์โพเนนเชียลช่วยให้บุคลากรทางการแพทย์เข้าใจถึงภัยคุกคามที่แฝงตัวอยู่และเตรียมการรับมือได้อย่างทันท่วงที

การกำหนดให้สถานการณ์การเพิ่มจำนวนเป็นจุดเน้นของเนื้อหาในหมวดหมู่การเปลี่ยนแปลงและความสัมพันธ์ไม่ได้หมายความว่านักเรียนที่เข้าร่วมการประเมินจะต้องมีความรู้เรื่องฟังก์ชันเอกซ์โพเนนเชียลมาก่อนและข้อสอบไม่ต้องใช้ความรู้เรื่องฟังก์ชันเอกซ์โพเนนเชียล แต่จะมีข้อสอบที่คาดหวังให้นักเรียนต้อง (1) ตระหนักรู้ว่าความสัมพันธ์ทุกความสัมพันธ์ไม่ได้เป็นเชิงเส้นเสมอไป (2) รู้ว่าการเพิ่มจำนวนแบบไม่เป็นเชิงเส้นมีความหมายโดยนัยที่เฉพาะและลึกซึ้งต่อความเข้าใจกับบางสถานการณ์ (3) เข้าใจเบื้องต้นในความหมายของการเพิ่มจำนวนแบบเอกซ์โพเนนเชียลว่าเป็นการเพิ่มขึ้นอย่างรวดเร็ว

ปริภูมิและรูปทรง

ปริภูมิและรูปทรงเกี่ยวข้องกับสถานการณ์ต่าง ๆ ที่มองเห็นได้ด้วยตาเปล่าหรือต้องอาศัยจินตนาการ เช่น แบบรูป สมบัติของวัตถุ ตำแหน่งและการกำหนดทิศทาง การแสดงแทนวัตถุต่าง ๆ การเข้ารหัสและถอดรหัสของข้อมูลที่ต้องอาศัยการนึกภาพ การมีปฏิสัมพันธ์กับรูปร่างต่าง ๆ ทั้งแบบจับต้องได้และแบบที่เป็นการแสดงแทน การเคลื่อนที่ การเปลี่ยนแปลงตำแหน่ง และความสามารถในการคาดหวังสิ่งที่จะเกิดขึ้นในปริภูมิ  เรขาคณิตเป็นพื้นฐานที่สำคัญสำหรับเนื้อหาปริภูมิและรูปทรง แต่เนื้อหาในหมวดหมู่นี้ขยายขอบเขตไปกว้างกว่าเนื้อหาสาระของเรขาคณิตทั่วไป ทั้งในแง่เนื้อหา ความหมาย และวิธีการ โดยมีการผนวกองค์ประกอบของคณิตศาสตร์สาขาอื่น ๆ เข้ามาด้วย เช่น การนึกภาพ การวัด และพีชคณิต

PISA มีสมมติฐานว่า ความเข้าใจแนวคิดและทักษะหลักมีความสำคัญต่อความฉลาดรู้ด้านคณิตศาสตร์ที่เชื่อมโยงกับปริภูมิและรูปทรง  โดยความฉลาดรู้ด้านคณิตศาสตร์ในเนื้อหาปริภูมิและรูปทรงเกี่ยวข้องกับกิจกรรมที่หลากหลาย เช่น ความเข้าใจเรื่องมุมมองในการวาดภาพ การสร้างและการอ่านแผนที่ การแปลงทางเรขาคณิตโดยใช้และไม่ใช้เทคโนโลยี การตีความภาพสามมิติจากมุมมองต่าง ๆ และการสร้างรูปต่าง ๆ

โลกทุกวันนี้เต็มไปด้วยสิ่งที่มีรูปหรือทรงแบบต่าง ๆ ไม่ใช่เฉพาะรูปหรือทรงที่มีความสมมาตรหรือมีแบบรูปปกติ เนื่องจากการหาพื้นที่หรือปริมาตรของสิ่งเหล่านี้ไม่สามารถใช้สูตรได้โดยตรง เช่น การหาพื้นที่สำหรับการปูพรมในตึกแห่งหนึ่งซึ่งมีมุมแหลมกับส่วนโค้งแคบ ๆ จะยากกว่าการหาพื้นที่ของห้องรูปสี่เหลี่ยม ดังนั้น ความเข้าใจในเรื่องการประมาณค่าเชิงเรขาคณิตจึงเป็นสิ่งที่จำเป็นในโลกยุคปัจจุบัน

การกำหนดให้การประมาณค่าเชิงเรขาคณิตเป็นจุดเน้นของเนื้อหาในหมวดหมู่ปริภูมิและรูปทรงนั้นเป็นการบ่งบอกถึงความจำเป็นสำหรับนักเรียนที่ต้องสามารถใช้ความเข้าใจในเรื่องของปริภูมิและรูปทรงในสถานการณ์ต่าง ๆ ที่หลากหลาย

ปริมาณ

แนวคิดเกี่ยวกับการแสดงปริมาณต่าง ๆ และการใช้ความรู้เกี่ยวกับปริมาณ ต้องมีความเข้าใจในเรื่องการวัด การนับ ขนาด หน่วยวัด ดัชนี การเปรียบเทียบขนาด และแนวโน้มและแบบรูปเชิงจำนวน  นอกจากนี้ การให้เหตุผลเชิงปริมาณ เช่น ความรู้สึกเชิงจำนวน การแสดงแทนจำนวนด้วยวิธีต่าง ๆ ความละเอียดรอบคอบในการคำนวณ การคิดเลขในใจ การประมาณค่า และการประเมินความสมเหตุสมผลของผลลัพธ์ ล้วนเป็นสิ่งจำเป็นของความฉลาดรู้ด้านคณิตศาสตร์ในเนื้อหาเรื่องปริมาณ

การแสดงปริมาณเป็นวิธีการขั้นพื้นฐานของการอธิบายและการวัดลักษณะต่าง ๆ ที่มีอยู่มากมายในโลก  ช่วยให้เราสร้างตัวแบบของสถานการณ์ต่าง ๆ  ตรวจสอบการเปลี่ยนแปลงและความสัมพันธ์ อธิบายและจัดการเกี่ยวกับปริภูมิและรูปทรง จัดการและตีความข้อมูล  ตลอดจนวัดและประเมินความไม่แน่นอน  ดังนั้น การมีความฉลาดรู้ด้านคณิตศาสตร์ในเนื้อหาปริมาณ จึงเป็นการนำความรู้เรื่องจำนวนและการดำเนินการของจำนวนไปใช้ในบริบทที่หลากหลาย

บางปัญหาที่พบทั้งในคณิตศาสตร์และสถิติไม่สามารถหาคำตอบได้โดยง่าย เนื่องจากต้องใช้ความรู้ทางคณิตศาสตร์ที่มีความซับซ้อน หรือเกี่ยวข้องกับปัจจัยต่าง ๆ เป็นจำนวนมาก หรือเนื่องจากประเด็นด้านจริยธรรมเกี่ยวกับผลกระทบต่อสิ่งมีชีวิตหรือสภาพแวดล้อม  ส่งผลให้ในปัจจุบันมีการใช้โปรแกรมสร้างแบบจำลองสถานการณ์ด้วยคอมพิวเตอร์ผ่านอัลกอริทึมมาช่วยแก้ปัญหา เราสามารถใช้โปรแกรมจำลองสถานการณ์ช่วยทำการคำนวณ โดยเราทำเพียงวางแผน ทำนาย และหาคำตอบของปัญหาโดยใช้ข้อมูลจากตัวแปรที่สามารถควบคุมได้ ดังนั้น ความเข้าใจในเรื่องการจำลองสถานการณ์ด้วยคอมพิวเตอร์จึงเป็นเรื่องที่มีความสำคัญในโลกยุคปัจจุบัน

การกำหนดให้การจำลองสถานการณ์ด้วยคอมพิวเตอร์เป็นจุดเน้นของเนื้อหาในหมวดหมู่ปริมาณนั้นเป็นการบ่งบอกว่าในบริบทการประเมินผลคณิตศาสตร์โดยใช้คอมพิวเตอร์ (Computer-Based Assessment of Mathematics : CBAM) ของ PISA ที่เริ่มใช้ในรอบการประเมิน PISA 2022 จะมีสถานการณ์ของปัญหาที่ซับซ้อนหลากหลายประเภทซึ่งรวมถึงการจัดทำงบประมาณและการวางแผนเรื่องอื่น ๆ โดยนักเรียนจะได้วิเคราะห์ตัวแปรต่าง ๆ ของปัญหานั้นโดยใช้การจำลองสถานการณ์ด้วยคอมพิวเตอร์ที่กำหนดให้

ความไม่แน่นอนและข้อมูล

ความแปรผันและความไม่แน่นอนเป็นเรื่องปกติของวิทยาศาสตร์ เทคโนโลยี และชีวิตประจำวัน และเป็นหัวใจของทฤษฎีความน่าจะเป็นและสถิติ  เนื้อหาในหมวดหมู่ความไม่แน่นอนและข้อมูลนี้รวมถึงการตระหนักรู้ถึงสถานการณ์ที่มีความแปรผันในชีวิตจริง  การมีความรู้สึกเชิงปริมาณของความแปรผันนั้น และการยอมรับถึงความไม่แน่นอนและความคลาดเคลื่อนในการอ้างอิงที่เกี่ยวข้อง  นอกจากนี้ยังรวมถึงการสร้าง การตีความ และการประเมินข้อสรุปในสถานการณ์ที่มีความไม่แน่นอนปรากฏอยู่ ดังนั้น การนำเสนอและ
การตีความข้อมูลจึงเป็นแนวคิดหลักของเนื้อหาในหมวดหมู่นี้

การคาดการณ์ทางเศรษฐศาสตร์ ผลการสำรวจความคิดเห็น และการพยากรณ์อากาศ สิ่งเหล่านี้ล้วนมีความแปรผันและความไม่แน่นอนปรากฏอยู่ด้วย  การแปรผันปรากฏอยู่ในกระบวนการผลิตเชิงอุตสาหกรรม คะแนนสอบ และผลการสำรวจ อีกทั้งการเสี่ยงโชคยังเป็นเรื่องพื้นฐานของกิจกรรมสันทนาการที่ผู้คนชื่นชอบ เนื้อหาความน่าจะเป็นและสถิติในหลักสูตรโดยทั่วไปจะให้วิธีการที่เป็นทางการในการอธิบาย การสร้างตัวแบบ และการตีความของปรากฏการณ์บางประเภทที่ความแปรผันมีบทบาทสำคัญ รวมถึงการอนุมานถึงสิ่งที่สอดคล้องกัน  นอกจากนี้ ความรู้เรื่องจำนวนและความรู้บางประการเกี่ยวกับพีชคณิต เช่น กราฟ และการแสดงแทนด้วยสัญลักษณ์ ยังช่วยสนับสนุนการแก้ปัญหาเกี่ยวกับเนื้อหาในหมวดหมู่นี้อีกด้วย

ในทางสถิติ เมื่อมีตัวแปรมากกว่าหนึ่งตัว ในแต่ละตัวแปรมีความแปรผัน และยังมีความแปรผันร่วมซึ่งบ่งบอกถึงความสัมพันธ์ระหว่างตัวแปรเหล่านั้น ความสัมพันธ์ระหว่างตัวแปรนี้โดยส่วนใหญ่สามารถแสดงได้ด้วยตารางสองทางซึ่งจะเป็นพื้นฐานในการตัดสินใจแบบมีเงื่อนไข (การอนุมาน) ความคาดหวังของข้อสอบ PISA คือ การที่นักเรียนจะสามารถอ่านข้อมูลที่เกี่ยวข้องจากตารางและมีความเข้าใจอย่างลึกซึ้งถึงความหมายของข้อมูลที่สกัดออกมา

การกำหนดให้การตัดสินใจแบบมีเงื่อนไขเป็นจุดเน้นของเนื้อหาในหมวดหมู่ความไม่แน่นอนและข้อมูลนั้นเป็นการบ่งบอกว่านักเรียนควรเข้าใจว่าการกำหนดวิธีการในการวิเคราะห์ข้อมูลในตัวแบบจะมีผลกระทบต่อข้อสรุปที่สามารถสร้างได้ และสมมติฐานหรือความสัมพันธ์ที่แตกต่างกันอาจส่งผลให้เกิดข้อสรุปที่แตกต่างกันด้วย

องค์ประกอบที่ 3 บริบท

จากนิยามของความฉลาดรู้ด้านคณิตศาสตร์นั้น มีประเด็นสำคัญที่ควรคำนึงถึงในการพัฒนาข้อสอบ PISA อยู่สองประเด็น ได้แก่ ประเด็นที่ 1 ความฉลาดรู้ด้านคณิตศาสตร์เกิดขึ้นในบริบทของชีวิตจริง  และประเด็นที่ 2 ความฉลาดรู้ด้านคณิตศาสตร์ช่วยให้บุคคลเข้าใจถึงบทบาทของคณิตศาสตร์ และตัดสินใจบนพื้นฐานของข้อมูลและเหตุผลที่เหมาะสม ซึ่งเป็นสิ่งจำเป็นสำหรับพลเมืองในศตวรรษที่ 21 ที่ต้องคิดอย่างไตร่ตรอง สร้างสรรค์ และมีส่วนร่วมต่อสังคมส่วนรวม  ในหัวข้อนี้จะกล่าวถึงบริบทในชีวิตจริงและทักษะแห่งศตวรรษที่ 21 ที่มีผลต่อการพัฒนาข้อสอบ

ประเภทของบริบท

ลักษณะสำคัญประการหนึ่งของความฉลาดรู้ด้านคณิตศาสตร์คือ การใช้คณิตศาสตร์เพื่อแก้ปัญหาในบริบทใดบริบทหนึ่ง ซึ่งบริบทคือ มุมมองในชีวิตจริงที่ปัญหาเหล่านั้นถูกกำหนดขึ้นมา ทั้งนี้ การเลือกใช้กลยุทธ์และการแสดงแทนทางคณิตศาสตร์ที่เหมาะสมมักจะขึ้นอยู่กับบริบทที่ปัญหานั้นเกิดขึ้น และมีความจำเป็นที่ต้องใช้ความรู้เกี่ยวกับบริบทในชีวิตจริงเพื่อพัฒนาตัวแบบทางคณิตศาสตร์ขึ้น  ดังนั้น สิ่งสำคัญในการประเมินของ PISA คือ การใช้บริบทที่หลากหลาย เพื่อเพิ่มความเป็นไปได้ที่จะมีบริบทที่สอดคล้องกับความสนใจของนักเรียนแต่ละคน และสอดคล้องกับสถานการณ์ต่าง ๆ ที่นักเรียนแต่ละคนจะได้พบเจอในศตวรรษที่ 21

ตามกรอบโครงสร้างการประเมินด้านคณิตศาสตร์ของ PISA 2022 ยังคงจัดประเภทของบริบทออกเป็น 4 กลุ่ม เช่นเดียวกับ PISA 2012 ดังนี้

• บริบทส่วนตัว (Personal context)  ปัญหาที่จัดอยู่ในบริบทส่วนตัวนี้เน้นที่กิจกรรมของบุคคล ครอบครัว หรือกลุ่มบุคคล เช่น บริบทที่เกี่ยวข้องกับการจัดเตรียมอาหาร การซื้อสินค้า การเล่นเกม  สุขภาพ การเดินทาง กิจกรรมสันทนาการ กีฬา การท่องเที่ยว การจัดตารางเวลา และการเงิน
• บริบทอาชีพ (Occupational context)  ปัญหาที่จัดอยู่ในบริบททางการงานอาชีพนี้เน้นที่โลกของการทำงาน เช่น บริบทที่เกี่ยวข้องกับการวัด การหาค่าใช้จ่ายและการจัดซื้อวัสดุสำหรับการก่อสร้าง บัญชีเงินเดือนหรือการบัญชี  การควบคุมคุณภาพ  การจัดตารางงานหรือการจัดทำรายการสินค้า  การออกแบบหรืองานสถาปัตยกรรม และการตัดสินใจที่เกี่ยวกับงานไม่ว่าจะใช้หรือไม่ได้ใช้เทคโนโลยีที่เหมาะสม บริบทอาชีพอาจเกี่ยวข้องกับแรงงานในทุกระดับตั้งแต่แรงงานไร้ฝีมือจนถึงแรงงานที่ต้องใช้ความเชี่ยวชาญระดับสูง
• บริบทสังคม (Societal context)  ปัญหาที่จัดอยู่ในบริบทสังคมนี้เน้นที่สังคมหนึ่ง ๆ ไม่ว่าจะเป็นระดับท้องถิ่น ระดับประเทศ หรือระดับโลก เช่น บริบทที่เกี่ยวข้องกับระบบการลงคะแนนเสียง การขนส่งสาธารณะ การปกครอง นโยบายภาครัฐ ข้อมูลประชากร การโฆษณา สุขภาพ ความบันเทิง ข้อมูลทางสถิติและเศรษฐกิจระดับชาติ แม้ว่าแต่ละบุคคลจะมีส่วนเกี่ยวข้องกับเรื่องดังกล่าวนี้ในระดับส่วนตัว แต่บริบทสังคมนี้จะเน้นการมองปัญหาเหล่านั้นในเชิงภาพรวมทางสังคมหรือชุมชน
• บริบทวิทยาศาสตร์ (Scientific context)  ปัญหาที่จัดอยู่ในบริบทวิทยาศาสตร์นี้เกี่ยวข้องกับการประยุกต์ใช้คณิตศาสตร์กับโลกธรรมชาติ และประเด็นหรือหัวข้อที่เกี่ยวข้องกับวิทยาศาสตร์และเทคโนโลยี เช่น บริบทที่เกี่ยวข้องกับสภาพอากาศหรือภูมิอากาศ นิเวศวิทยา การแพทย์ วิทยาศาสตร์อวกาศ พันธุศาสตร์ การวัด และคณิตศาสตร์ โดยข้อสอบที่เป็นเรื่องเฉพาะของคณิตศาสตร์จะถูกรวมอยู่ในบริบทวิทยาศาสตร์ด้วย

ทักษะแห่งศตวรรษที่ 21

ทักษะแห่งศตวรรษที่ 21 เป็นทักษะหนึ่งที่ทั่วโลกให้ความสนใจเพิ่มมากขึ้น และมักจะรวมทักษะนี้ไว้ในการจัดการศึกษา สิ่งสำคัญสำหรับการศึกษาในปัจจุบันนี้คือ ต้องเตรียมความพร้อมให้นักเรียนมีเครื่องมือที่สามารถใช้ปกป้องตัวเองจากการหลอกลวงและการลงข้อสรุปที่กล่าวอ้างว่ามีพื้นฐานมาจากการให้เหตุผลทางคณิตศาสตร์  ซึ่งบ่อยครั้งความชำนาญในการใช้เหตุผลอย่างสมเหตุสมผลก็เป็นเครื่องมือที่เพียงพอแล้ว เนื่องจากการหลอกหลวงมักจะมีข้อมูลที่ขัดแย้งกันแอบแฝงไว้ด้วย  การเรียนรู้คณิตศาสตร์จะช่วยพัฒนาให้เยาวชนมีความพร้อมในการรับมือกับข้อมูลที่มีความขัดแย้งแอบแฝงอยู่

ความเชื่อมโยงกันระหว่างทักษะแห่งศตวรรษที่ 21 และทักษะเฉพาะที่เกี่ยวข้องกับการเรียนรู้เนื้อหาทางคณิตศาสตร์ ได้ถูกนำมาผนวกไว้ในกรอบการประเมิน PISA 2022  จำนวน 8 ทักษะ ดังนี้

• การคิดอย่างมีวิจารณญาณ (Critical thinking)
• ความคิดสร้างสรรค์ (Creativity)
• การค้นคว้าและสืบเสาะหาความรู้ (Research and inquiry)
• การนำตนเอง การคิดริเริ่ม และความมุมานะ (Self-direction, initiative, and persistence)
• การใช้สารสนเทศ (Information use)
• การคิดเชิงระบบ (Systems thinking)
• การสื่อสาร (Communication)
• การคิดอย่างไตร่ตรอง (Reflection)

---

ข้อมูลเพิ่มเติม

OECD (2023), PISA 2022 Assessment and Analytical Framework, PISA, OECD Publishing, Paris, https://doi.org/10.1787/dfe0bf9c-en.